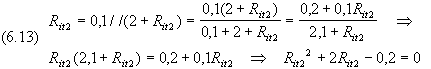|
|
|
|
Esempio 6.5 Determinare l’impedenza
iterativa di uscita del quadripolo di fig. 6.21a. Verificare la correttezza del
risultato ottenuto. 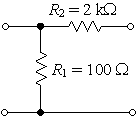
Fig. 6.21- Esempio 6.4. Soluzione L’impedenza di
ingresso è pari a Ri = R1//(R2+ RL); imponendo la condizione Rit2
= R1//(R2 + Rit2)
e risolvendo l’equazione si ottiene l’impedenza iterativa di uscita Rit2.
Esprimendo le resistenze in k si ha si ha 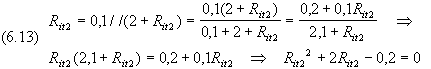
Le soluzioni dell’equazione
sono -2,095 k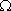 e 0,0954 k e 0,0954 k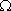 ; scartando la prima perché negativa, si ottiene Rit2= 95,4 ; scartando la prima perché negativa, si ottiene Rit2= 95,4 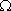 . Verifica: 0,1//(2 + 0,0954) = 0,0954. . Verifica: 0,1//(2 + 0,0954) = 0,0954. |
| |
| Procedura per la creazione di una funzione par(x,y) che calcoli il parallelo di due impedenze (o la serie di due ammettenze): - editare un file di testo dal seguente contenuto: function p=par(x,y) %PAR Impedenza equivalente parallelo (ammettenza equivalente serie) % PAR(X,Y) calcola l'impedenza equivalente parallelo (l’ammettenza % equivalente serie) corrispondente ai due valori di ingresso X,Y p=(x.*y)./(x+y); - salvare il file come par.m in una directory riconosciuta da Matlab (ad es.
...\matlab\toolbox\matlab\elfun) | |
| |
| Tab. 1 |
| |
Calcolo delle soluzioni dell’equazione
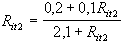 | solve('R=(.2+.1*R)/(2.1+R)') | | Output | ans =
[ -2.0954451150103322269139395656016]
[ .95445115010332226913939565601604e-1] | | Verifica: Rit2 = R1//(R2 + Rit2) | par(.1,2+.0954) | | Output | ans =
0.0954 | |
| |
| Tab. 2 |
|
| |
Esempio 6.6 Determinare le impedenze
immagini del quadripolo di fig. 6.21a. Verificare la correttezza dei risultati
ottenuti. Soluzione Le impedenze immagini si
ottengono imponendo Ri = RI1 e Ru= RI2. Applicando tali condizioni al quadripolo
considerato si ottiene il sistema 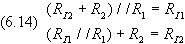
la cui soluzione a
valori positivi è RI1 = 97,6 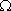 e RI2= 2,049 k
e RI2= 2,049 k . . |
| |
| Calcolo delle soluzioni del sistema 6.14 | [R1,R2]=solve('((R2+2)*.1)/(R2+2+.1)=R1',...
'(R1*.1)/(R1+.1)+2=R2') | | Output | R1 =
[ -.97590007294853317935438463624010e-1]
[ .97590007294853317935438463624010e-1]
R2 =
[ -2.0493901531919196766442077361042]
[ 2.0493901531919196766442077361042] | | Verifica: RI1 = R1//(R2 + RI2) | par(2.049+2,.1) | | Output | ans =
0.0976 | | Verifica: RI2 = R2 + (R1//RI1) | par(0.0976,.1)+2 | | Output | ans =
2.0494 | |
| |
| Tab. 3 |
|
| |
Esempio 6.7 Determinare l’impedenza
caratteristica del quadripolo di fig. 6.6b. 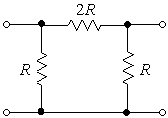
Fig. 6.6 -
Soluzione alternativa dell’esempio 6.1. Soluzione Imponendo [(R0//R)
+ 2R]//R = R0 e risolvendo l’equazione si
ottiene 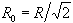 . . |
| |
Calcolo delle soluzioni dell’equazione
[(R0//R)
+ 2R]//R = R0 | solve('(((R0*R)/(R0+R)+2*R)*R)/((R0*R)/
(R0+R)+2*R+R)=R0','R0') (tutto di seguito) | | Output | ans =
[ 1/2*2^(1/2)*R]
[ -1/2*2^(1/2)*R] | |
| |
| Tab. 4 |
|