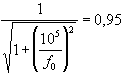|
|
|
|
Esempio 8.1
Tracciare i diagrammi di Bode di
un filtro passa-basso il cui guadagno complesso è
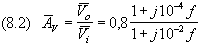
Determinare l’ordine del filtro
e il valore della frequenza di taglio.
Soluzione
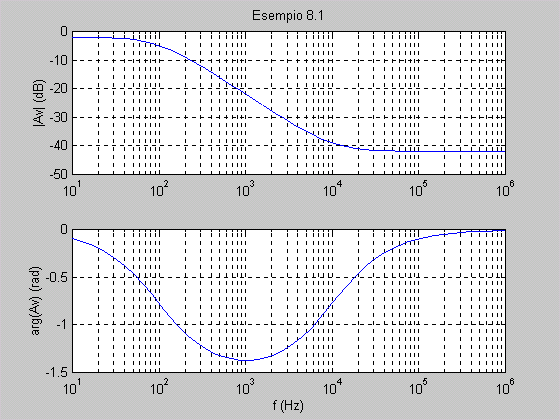
I diagrammi di Bode si ottengono
rappresentando graficamente su scala delle frequenze logaritmica le funzioni 20logAV
e arg(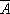 V). Dal primo dei due
diagrammi si desume che il filtro è del 1° ordine, dato che la pendenza della
curva è pari a 20 dB/decade. Alle basse frequenze si ha AV0
= 0,8; risolvendo l’equazione AV(f) = 0,8/ V). Dal primo dei due
diagrammi si desume che il filtro è del 1° ordine, dato che la pendenza della
curva è pari a 20 dB/decade. Alle basse frequenze si ha AV0
= 0,8; risolvendo l’equazione AV(f) = 0,8/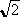 si determina la frequenza di taglio del filtro, pari a
f0 =
100 Hz. si determina la frequenza di taglio del filtro, pari a
f0 =
100 Hz. |
| |
| Definizione del vettore f a 50 valori logaritmicamente spaziati tra 10 e 106 |
f=logspace(1,6); |
| Definizione del vettore complesso 8.2 (in MATLAB
ie
j sono variabili predefinite come unità immaginarie) |
A=.8*(1+i*.0001*f)./(1+i*.01*f); |
| Suddivisione della figura in due finestre e selezione della finestra 1 |
subplot(2,1,1) |
| Esecuzione del grafico su scala orizzontale logaritmica
f - AV(dB) |
semilogx(f,20*log10(abs(A))) |
| Visualizzazione della griglia |
grid |
| Inserimento del titolo |
title('Esempio 8.1') |
| Inserimento dell’etichetta sull’asse verticale |
ylabel('|Av| (dB)') |
| Selezione della finestra 2 |
subplot(2,1,2) |
Esecuzione del grafico su scala orizzontale logaritmica
f - 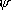 |
semilogx(f,angle(A)) |
| Visualizzazione della griglia |
grid |
| Inserimento dell’etichetta sull’asse orizzontale |
xlabel('f (Hz)') |
| Inserimento dell’etichetta sull’asse verticale |
ylabel('arg(Av) (rad)') |
| |
|
| Calcolo della frequenza di taglio del filtro |
solve('.8*sqrt(1+(.0001*f)^2)/
sqrt(1+(.01*f)^2)=.8/sqrt(2)')
(tutto di seguito) |
| Output |
ans =
[ -100.01000150025004375787644401818]
[ 100.01000150025004375787644401818]
|
|
| |
| Tab. 1 |
| |
|
|
|
| |
| Esempio 8.2 Dimensionare
un filtro RC passa-basso avente un guadagno costante fino a 100 kHz entro un
margine del 5%.
Soluzione
Poiché
alle basse frequenze il guadagno è pari a 1, per rispettare il margine indicato
si deve avere un guadagno a 100 kHz pari a 0,95. Imponendo
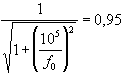
e risolvendo l’equazione si ottiene f0 =
304 kHz. Scegliendo arbitrariamente C = 1 nF, la frequenza di taglio
desiderata si ottiene con una resistenza R tale che 304 · 103 = 1/(2 R · 10-9) da cui
R = 1/(2 R · 10-9) da cui
R = 1/(2 ·
304 · 103 · 10-9) = 524 ·
304 · 103 · 10-9) = 524 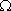 . .
|
| |
| Calcolo delle soluzioni dell’equazione precedentemente riportata |
solve('1/sqrt(1+(10^5/f)^2)=.95') |
| Output | ans =
[ -304243.49222966555361818197255861]
[ 304243.49222966555361818197255861] |
|
| |
| Tab. 2 |
|
| |
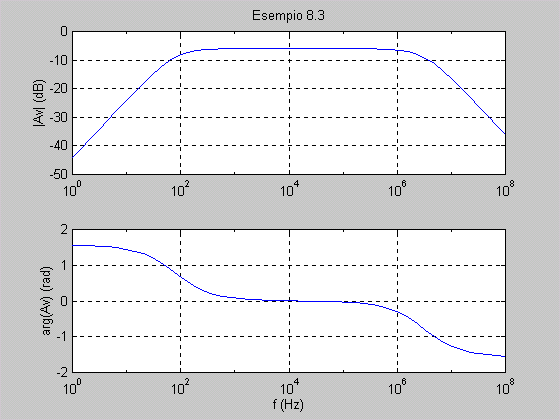
Esempio 8.3 Tramite due filtri RC
in cascata, il primo di tipo passa-basso, il secondo di tipo
passa-alto con frequenza di taglio inferiore a quella del primo, è
possibile realizzare un filtro passa-banda (fig. 8.13). Il guadagno
complessivo del filtro, pur essendo pari al prodotto dei guadagni
parziali, non può essere ottenuto moltiplicando le espressioni 8.10
e 8.17, dato che la prima delle due è ottenuta a circuito aperto,
mentre in questo caso il filtro passa-basso è chiuso sul secondo
quadripolo che gli fa da carico; ciononostante, dallo studio che
segue si può notare che il circuito si comporta, almeno
qualitativamente, come se i due filtri non si influenzassero tra di
loro; si noti il valore del guadagno a centro banda, pari a 0,5,
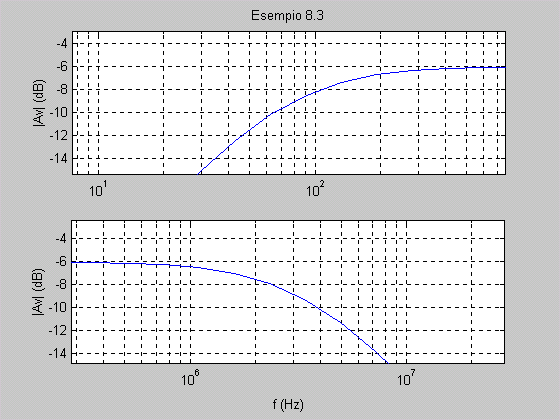
ovvero -6 dB. Se si osserva il grafico da vicino nella sezione zoom
si possono determinare i valori approssimativi delle frequenze di
taglio, alle quali AV
è pari a -9dB: f1
 80 Hz, f2 80 Hz, f2
 3 MHz. 3 MHz.
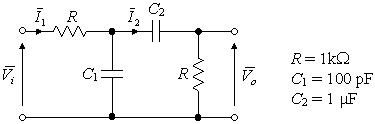
Fig. 8.13 - Esempio 8.3.
|
| |
| Definizione del vettore f a 50 valori logaritmicamente spaziati tra 1 e 108 | f=logspace(0,8); | | Definizione di R | R=1000; | | Definizione di C1 | C1=1e-10; | | Definizione di C2 | C2=1e-6; | | Definizione del vettore impedenza associato alla capacità C1 | Z1=-i./(2*pi*f*C1); | | Definizione del vettore impedenza associato alla capacità C2 | Z2=-i./(2*pi*f*C2); | Definizione del vettore corrente 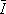 1 (la corrente 1 (la corrente 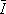 1, avendo posto 1, avendo posto 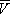 i = 1, è pari a i = 1, è pari a 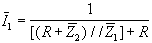
Si noti l’utilizzo della funzione par, definita nell’esempio 6.5 | I1=1./(par(Z2+R,Z1)+R); | Definizione del vettore 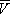 o, pari a o, pari a 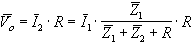
Avendo posto 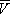 i = 1, i = 1, 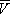 o coincide con o coincide con 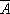 V = V = 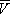 o/ o/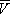 i i | Vo=I1*R.*Z1./(Z1+Z2+R); | | Suddivisione della figura in due finestre e selezione della finestra 1 | subplot(2,1,1) | | Esecuzione del grafico su scala orizzontale logaritmica f - AV(dB) | semilogx(f,20*log10(abs(Vo))) | | Visualizzazione della griglia | grid | | Inserimento del titolo | title('Esempio 8.3') | | Inserimento dell’etichetta sull’asse verticale | ylabel('|Av| (dB)') | | Selezione della finestra 2 | subplot(2,1,2) | Esecuzione del grafico su scala orizzontale logaritmica f - 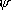 | semilogx(f,angle(Vo)) | | Visualizzazione della griglia | grid | | Inserimento dell’etichetta sull’asse orizzontale | xlabel('f (Hz)') | | Inserimento dell’etichetta sull’asse verticale | ylabel('arg(Av) (rad)') | | Attivazione dello zoom sulla figura mediante mouse | zoom |
|
| |
| Tab. 3 |
| |
| Il comando zoom
attiva lo zoom-in e lo zoom-out su un grafico 2-D. Quando zoom
è ON, cliccando sul grafico con il tasto sinistro (destro) del mouse
si attiva lo zoom-in (zoom-out) della zona intorno al puntatore del
mouse. |
| |
|
|
| |
|
|
|